Dalam tutorial GNU R Cepat ini untuk model statistik dan grafik kami akan memberikan contoh regresi linear yang mudah dan belajar bagaimana untuk melaksanakan analisis statistik asas data. Analisis ini akan disertakan dengan contoh grafik, yang akan membawa kita lebih dekat untuk menghasilkan plot dan carta dengan gnu r. Sekiranya anda tidak biasa dengan menggunakan R, sila lihat tutorial prasyarat: tutorial GNU R yang cepat untuk operasi asas, fungsi dan struktur data.

Model dan formula dalam r

Kami faham a model dalam statistik sebagai penerangan ringkas data. Pembentangan data seperti itu biasanya dipamerkan dengan a Formula matematik. R mempunyai cara tersendiri untuk mewakili hubungan antara pembolehubah. Contohnya, hubungan berikut y = c₀+c₁x₁+c₂x₂+... +c_nx_n+r dalam r ditulis sebagai

y ~ x1+x2+...+xn,

yang merupakan objek formula.

Contoh regresi linear

Marilah kita memberikan contoh regresi linear untuk gnu r, yang terdiri daripada dua bahagian. Pada bahagian pertama contoh ini, kita akan mengkaji hubungan antara pulangan indeks kewangan yang didenominasikan dalam dolar AS dan pulangan tersebut didenominasikan dalam dolar Kanada. Di samping itu, di bahagian kedua contohnya, kami menambah satu lagi pemboleh ubah kepada analisis kami, yang pulangan indeks yang didenominasikan dalam euro.

Regresi linear mudah

Muat turun Fail Data Contoh ke direktori kerja anda: Regresi-Example-GNU-R.CSV

Mari kita jalankan R di Linux dari lokasi direktori kerja hanya dengan

$ R

dan baca data dari fail data contoh kami:

> pulangan<-read.csv("regression-example-gnu-r.csv",header=TRUE)

Anda dapat melihat nama -nama pembolehubah menaip

> Nama (pulangan)
[1] "Amerika Syarikat" "Kanada" "Jerman"

Sudah tiba masanya untuk menentukan model statistik kami dan menjalankan regresi linear. Ini boleh dilakukan dalam beberapa baris kod berikut:

> y<-returns[,1]
> x1<-returns[,2]
> pulangan.lm<-lm(formula=y~x1)

Untuk memaparkan ringkasan analisis regresi, kami melaksanakannya ringkasan () berfungsi pada objek yang dikembalikan pulangan.lm. Itu dia,

> ringkasan (pulangan.lm)
Hubungi:
lm (formula = y ~ x1)
Sisa:
Min 1q median maksimum 3q
-0.038044 -0.001622 0.000001 0.001631 0.050251
Koefisien:
Anggarkan std. Ralat T Nilai PR (> | T |)
(Memintas) 3.174E-05 3.862E-05 0.822 0.411
x1 9.275E-01 4.880E-03 190.062 <2e-16 ***
---
Signif. Kod: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Kesalahan standard sisa: 0.003921 pada 10332 darjah kebebasan
R-kuadrat berganda: 0.7776, diselaraskan r-kuadrat: 0.7776
F-Statistik: 3.612e+04 pada 1 dan 10332 df, p-nilai: < 2.2e-16

Fungsi ini menghasilkan hasil yang sepadan di atas. Pekali anggaran di sini c₀~ 3.174E-05 dan c₁ ~ 9.275E-01. Nilai p di atas menunjukkan bahawa anggaran memintas c₀ tidak jauh berbeza dengan sifar, oleh itu ia boleh diabaikan. Koefisien kedua jauh berbeza daripada sifar sejak nilai p<2e-16. Therefore, our estimated model is represented by: y=0.93 x₁. Selain itu, R-kuadrat adalah 0.78, yang bermaksud kira -kira 78% varians dalam pembolehubah y dijelaskan oleh model.

Regresi linear berganda

Marilah kita menambah satu lagi pemboleh ubah ke dalam model kami dan melakukan analisis regresi berganda. Persoalannya sekarang ialah sama ada menambah satu lagi pemboleh ubah kepada model kami menghasilkan model yang lebih dipercayai.

> x2<-returns[,3]
> pulangan.lm<-lm(formula=y~x1+x2)
> ringkasan (pulangan.lm)
Hubungi:
lm (formula = y ~ x1 + x2)
Sisa:
Min 1q median maksimum 3q
-0.0244426 -0.0016599 0.0000053 0.0016889 0.0259443
Koefisien:
Anggarkan std. Ralat T Nilai PR (> | T |)
(Memintas) 2.385E-05 3.035E-05 0.786 0.432
x1 6.736E-01 4.978E-03 135.307 <2e-16 ***
x2 3.026E-01 3.783E-03 80.001 <2e-16 ***
---
Signif. Kod: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.'0.1 "1
Kesalahan standard sisa: 0.003081 pada 10331 darjah kebebasan
R-kuadrat berganda: 0.8627, diselaraskan r-kuadrat: 0.8626
F-Statistik: 3.245e+04 pada 2 dan 10331 df, p-nilai: < 2.2e-16

Di atas, kita dapat melihat hasil analisis regresi berganda selepas menambahkan pembolehubah x₂. Pembolehubah ini mewakili pulangan indeks kewangan dalam euro. Kami kini memperoleh model yang lebih dipercayai, kerana R-kuadrat yang diselaraskan adalah 0.86, yang lebih besar maka nilai yang diperoleh sebelum sama dengan 0.76. Perhatikan, bahawa kami membandingkan R-kuadrat yang diselaraskan kerana ia mengambil bilangan nilai dan saiz sampel ke dalam akaun. Sekali lagi pekali intercept tidak penting, oleh itu, model anggaran boleh diwakili sebagai: y = 0.67x₁+0.30x₂.

Perhatikan juga bahawa kami boleh merujuk kepada vektor data kami dengan nama mereka, contohnya

> lm (pulangan $ usa ~ pulangan $ canada)
Hubungi:
LM (formula = pulangan $ usa ~ pulangan $ canada)
Koefisien:
(Memintas) mengembalikan $ canada
3.174E-05 9.275E-01

Grafik

Dalam bahagian ini kita akan menunjukkan cara menggunakan r untuk visualisasi beberapa sifat dalam data. Kami akan menggambarkan angka yang diperolehi oleh fungsi seperti plot (), boxplot (), hist (), qqnorm ().

Plot bersepah

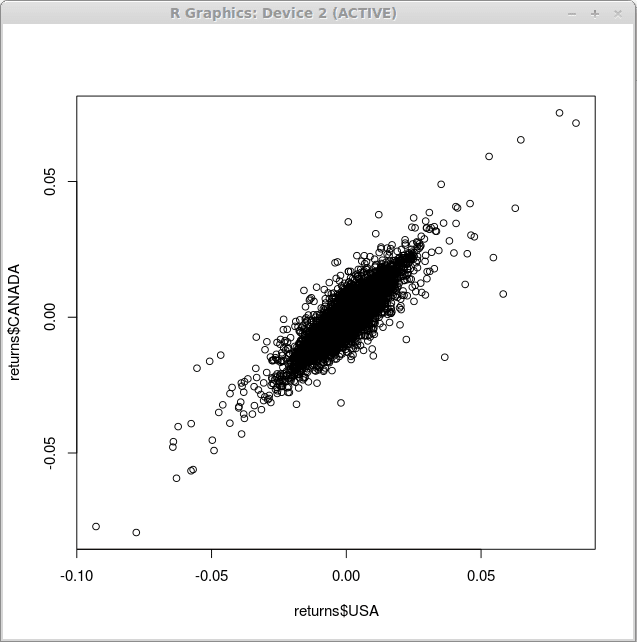
Mungkin yang paling mudah dari semua graf yang anda boleh dapatkan dengan r adalah plot penyebaran. Untuk menggambarkan hubungan antara denominasi dolar AS pulangan indeks kewangan dan denominasi dolar Kanada kita menggunakan fungsi tersebut plot () seperti berikut:

> Plot (pulangan $ usa, pulangan $ canada)

Hasil daripada pelaksanaan fungsi ini, kita memperoleh gambarajah penyebaran seperti yang dipamerkan di bawah

Salah satu hujah terpenting yang boleh anda lalui ke fungsi plot () adalah 'jenis'. Ia menentukan jenis plot yang perlu ditarik. Jenis yang mungkin adalah:
• '"p"'Untuk *p *oints
• '"L"'Untuk *l *ines
• '"b"' untuk kedua-dua
• '"c"'Untuk bahagian baris sahaja'" B "'
• '"o"'Untuk kedua -duanya'*o*bercerita '
• '"h"'Untuk'*h*istogram 'seperti (atau' ketumpatan tinggi ') garis menegak
• '"s"'Untuk tangga *s *teps
• '"S"'Untuk jenis lain *s *teps
• '"n"'Kerana tidak merancang
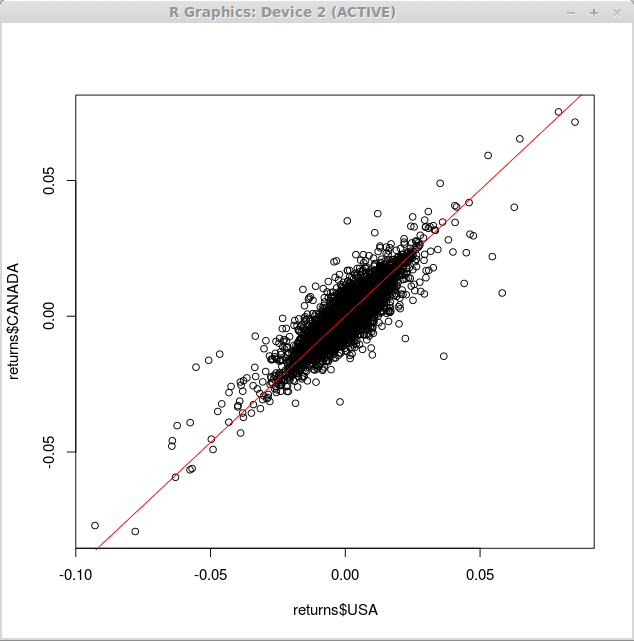
Untuk melapisi garis regresi ke atas gambarajah penyebaran di atas kita menggunakan lengkung () berfungsi dengan argumen 'tambah' dan 'col', yang menentukan bahawa garis harus ditambah ke plot yang ada dan warna garis yang diplot, masing -masing.

> lengkung (0.93*x, -0.1,0.1, tambah = benar, col = 2)

Oleh itu, kami memperoleh perubahan berikut dalam graf kami:

Untuk maklumat lanjut mengenai plot fungsi () atau garisan () Gunakan fungsi Tolong (), contohnya

> Bantuan (plot)

Plot kotak

Marilah kita melihat cara menggunakannya boxplot () berfungsi untuk menggambarkan statistik deskriptif data. Pertama, menghasilkan ringkasan statistik deskriptif untuk data kami oleh ringkasan () berfungsi dan kemudian melaksanakan boxplot () berfungsi untuk pulangan kami:

> Ringkasan (pulangan)
Amerika Syarikat Kanada Jerman
Min. : -0.0928805 min. : -0.0792810 min. : -0.0901134
1st qu.: -0.0036463 1st Qu.: -0.0038282 1st Qu.: -0.0046976
Median: 0.0005977 median: 0.0005318 median: 0.0005021
Maksud: 0.0003897 bermaksud: 0.0003859 bermaksud: 0.0003499
3rd qu.: 0.0046566 3rd qu.: 0.0047591 3rd qu.: 0.0056872
Maks. : 0.0852364 Max. : 0.0752731 Max. : 0.0927688 

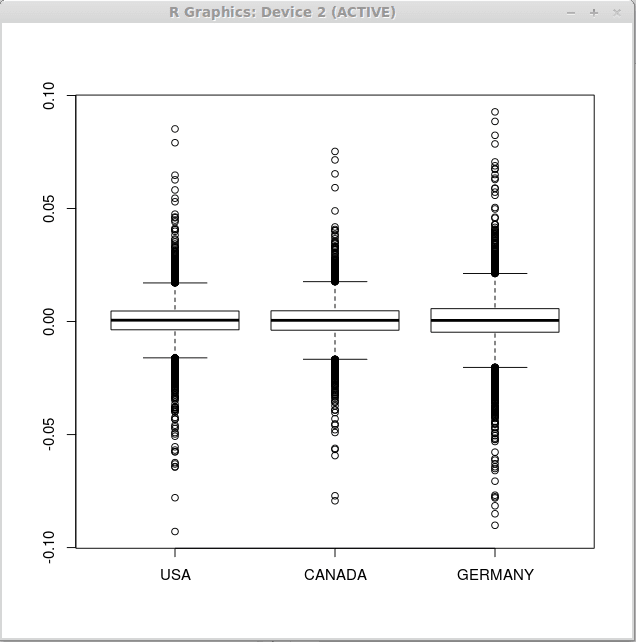
Perhatikan bahawa statistik deskriptif adalah serupa untuk ketiga -tiga vektor, oleh itu kita boleh mengharapkan kotak -kotak yang serupa untuk semua set pulangan kewangan. Sekarang, laksanakan fungsi boxplot () seperti berikut

> boxplot (pulangan)

Akibatnya, kami memperoleh tiga kotak berikut.

Histogram

Dalam bahagian ini kita akan melihat histogram. Histogram frekuensi telah diperkenalkan dalam Pengenalan kepada GNU R pada Sistem Operasi Linux. Sekarang kita akan menghasilkan histogram ketumpatan untuk pulangan yang dinormalisasi dan membandingkannya dengan lengkung ketumpatan biasa.

Marilah kita, pertama, menormalkan pulangan indeks yang didenominasikan dalam dolar AS untuk mendapatkan sifar min dan varians sama dengan satu untuk dapat membandingkan data sebenar dengan fungsi ketumpatan normal standard teoretikal.

> retus.norma<-(returns$USA-mean(returns$USA))/sqrt(var(returns$USA))
> bermaksud (retus.norma)
[1] -1.053152E-17
> var (retus.norma)
[1] 1

Sekarang, kami menghasilkan histogram ketumpatan untuk pulangan yang dinormalisasi dan plot lengkung ketumpatan normal standard ke atas histogram tersebut. Ini dapat dicapai dengan ungkapan r berikut

> hist (retus.norma, pecah = 50, freq = palsu)
> lengkung (dnorm (x),-10,10, tambah = benar, col = 2)

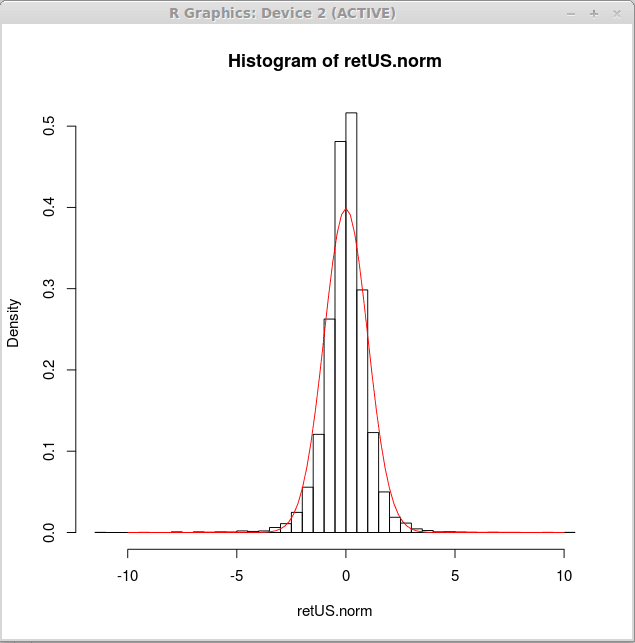
Secara visual, lengkung normal tidak sesuai dengan data dengan baik. Pengagihan yang berbeza mungkin lebih sesuai untuk pulangan kewangan. Kami akan belajar bagaimana untuk menyesuaikan pengedaran kepada data dalam artikel kemudian. Pada masa ini kita dapat menyimpulkan bahawa pengedaran yang lebih sesuai akan lebih banyak dipilih di tengah dan akan mempunyai ekor yang lebih berat.

QQ-plot

Satu lagi graf berguna dalam analisis statistik ialah plot QQ. Plot QQ adalah plot kuantil kuantil, yang membandingkan kuantil ketumpatan empirikal ke kuantil ketumpatan teoritis. Sekiranya perlawanan ini dapat melihat garis lurus. Marilah kita membandingkan pengedaran sisa yang diperolehi oleh analisis regresi kami di atas. Pertama, kita akan mendapatkan plot QQ untuk regresi linear yang mudah dan kemudian untuk regresi linear berganda. Jenis plot QQ yang akan kami gunakan adalah plot QQ biasa, yang bermaksud bahawa kuantil teoretikal dalam graf sesuai dengan kuantil pengedaran normal.

Plot pertama yang sepadan dengan sisa regresi linear mudah diperolehi oleh fungsi qqnorm () Dengan cara berikut:

> pulangan.lm<-lm(returns$US~returns$CANADA)
> qqnorm (pulangan.sisa $ $)

Grafik yang sepadan dipaparkan di bawah:

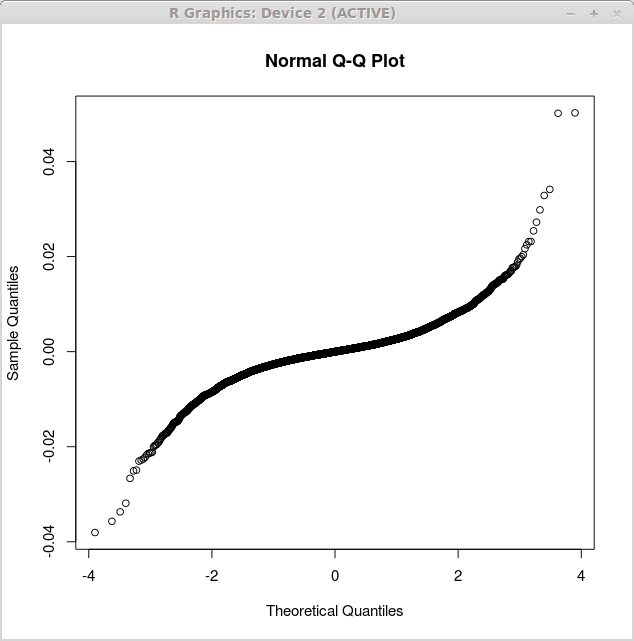
Plot kedua sepadan dengan sisa regresi linear berganda dan diperolehi sebagai:

> pulangan.lm<-lm(returns$US~returns$CANADA+returns$GERMANY)
> qqnorm (pulangan.sisa $ $)

Plot ini dipaparkan di bawah:

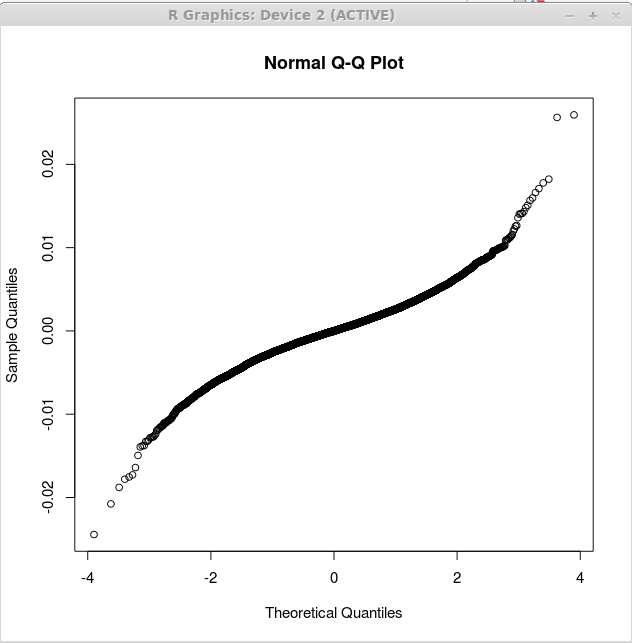
Perhatikan bahawa plot kedua lebih dekat dengan garis lurus. Ini menunjukkan bahawa sisa -sisa yang dihasilkan oleh analisis regresi berganda lebih dekat dengan diedarkan secara normal. Ini menyokong model kedua sebagai lebih berguna terhadap model regresi pertama.

Kesimpulan

Dalam artikel ini, kami telah memperkenalkan pemodelan statistik dengan gnu r mengenai contoh regresi linear. Kami juga telah membincangkan beberapa graf statistik yang sering digunakan. Saya harap ini telah membuka pintu kepada analisis statistik dengan gnu r untuk anda. Kami akan, dalam artikel kemudian, membincangkan aplikasi R yang lebih kompleks untuk pemodelan statistik serta pengaturcaraan sehingga terus membaca.

Siri Tutorial GNU R:

Bahagian I: Tutorial Pengenalan Gnu R:

1. Pengenalan kepada Gnu R pada Sistem Operasi Linux
2. Menjalankan Gnu R pada Sistem Operasi Linux
3. Tutorial Gnu R Cepat ke Operasi Asas, Fungsi dan Struktur Data
4. Tutorial Gnu R Cepat ke Model dan Grafik Statistik
5. Cara memasang dan menggunakan pakej dalam gnu r
6. Membina pakej asas dalam gnu r

Bahagian II: Bahasa Gnu R:

1. Gambaran keseluruhan bahasa pengaturcaraan GNU

Tutorial Linux Berkaitan:

• Pengenalan kepada Automasi, Alat dan Teknik Linux
• Perkara yang hendak dipasang di Ubuntu 20.04
• Menguasai Gelung Skrip Bash
• Perkara yang perlu dilakukan setelah memasang ubuntu 20.04 Focal Fossa Linux
• Gelung bersarang dalam skrip bash
• Mint 20: Lebih baik daripada Ubuntu dan Microsoft Windows?
• Mengendalikan input pengguna dalam skrip bash
• Ubuntu 20.04 Trik dan Perkara yang Anda Tidak Tahu
• Manipulasi data besar untuk keseronokan dan keuntungan bahagian 1
• Ubuntu 20.04 Panduan