Asas matematik komputer binari, perpuluhan, heksadesimal, oktal
- 1038
- 36
- Dana Hammes
Bagaimana kita menyatakan nombor bergantung kepada sama ada kita adalah komputer atau manusia. Sekiranya kita manusia, kita mungkin akan menyatakan nombor menggunakan biasa 10-asas Sistem perpuluhan. Sekiranya kita adalah komputer, kita mungkin, di teras kita, untuk menyatakan nombor sebagai 2-asas atau binari.
Jadi apa yang ada dengan semua cara untuk menyatakan nombor, dan mengapa mereka wujud? Artikel ini akan terperinci dan diharapkan pada akhirnya anda akan menghitung oktal pada jari anda. Yang berfungsi dengan baik, selagi anda hanya menggunakan 8 jari, selepas semua ... oktal adalah 8-asas.
Dalam tutorial ini anda akan belajar:
- Cara melakukan pengiraan mudah dalam sistem bukan decimal seperti binari, heksadesimal dan oktal.
- Apa istilah 2-base, 10-asas dll. berdiri dan bagaimana untuk memahaminya dengan lebih mudah.
- Sambungan antara pelbagai kaedah ini mengekspresikan nombor
Asas matematik komputer: binari, perpuluhan, heksadesimal, oktal Keperluan perisian dan konvensyen yang digunakan
| Kategori | Keperluan, konvensyen atau versi perisian yang digunakan |
|---|---|
| Sistem | Pengedaran linux-bebas |
| Perisian | Baris perintah bash, sistem berasaskan linux |
| Yang lain | Sebarang utiliti yang tidak termasuk dalam shell bash secara lalai boleh dipasang menggunakan sudo apt-get memasang nama utiliti (atau pemasangan yum untuk sistem berasaskan redhat) |
| Konvensyen | # - memerlukan komando linux untuk dilaksanakan dengan keistimewaan akar sama ada secara langsung sebagai pengguna root atau dengan menggunakan sudo perintah$-Memerlukan komando linux untuk dilaksanakan sebagai pengguna yang tidak istimewa |
Perpuluhan
Kita semua sangat akrab dengan sistem perpuluhan: 1 hingga 10 atau lebih baik 0 hingga 9, Sistem yang kami fikirkan dari hari paling awal sekolah dan bahkan sebelum ini oleh ibu bapa kami. Tetapi sistem berangka ini tidak semuanya ada. Ianya hanya salah seorang daripada mereka. Kami memanggil sistem ini 10-asas kerana ia mempunyai asas 10 aksara iaitu 0 hingga 9.
Dalam perpuluhan, kita boleh mengira dengan mudah dengan hanya menggunakan apa yang kita fikirkan: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Kita tidak perlu berusaha untuk ini, dan secara semula jadi. Walau bagaimanapun, jika anda benar -benar memikirkannya, tidak ada hubungan logik sebenar antara nombor perkataan "sifar" dan "satu" dan "satu" dan "dua" dan sebagainya. Offcourse, pada waktunya kita memahami perkara itu 0+1 = 1 dan 1+1 = 2, Tetapi tidak ada yang nyata dan besar langsung yang lain Sambungan antara satu hingga dua, 1 dan 2. Ia hanya satu bentuk ungkapan.
Untuk mencontohkan ini, pertimbangkan pernyataan di atas berbanding dengan fiktif 5-asas sistem. Jauh lebih sukar untuk minda kita, kerana mereka belum dilatih dalam hal yang sama, untuk dikira dalam sistem 5-asas. Mari kita buat satu langkah lebih keras dan nyatakan bahawa 5 nombor kita dinyatakan sebagai (, ), +, = dan . masing -masing. Mari kita hitung hingga 11 akan kita?
0: (1 :) 2: + 3: = 4: . 5 :) (6 :)) 7 :)+ 8 :) = 9 :). 10: +(11: +)
Di sebelah kiri kita mempunyai nombor perpuluhan 10-asas, di sebelah kanan kita mempunyai sistem angka 5-asas yang dihasilkan sendiri dengan cara yang sama (dan kedua-dua kiri dan kanan mempunyai nilai berangka yang sama, i.e. 10 dalam perpuluhan/10-asas adalah +( dalam sistem berangka 5 asas kami!).
Saya boleh mengira dengan mudah dengan cara ini kerana saya sangat biasa dengan cara X-base sistem berfungsi. Sekiranya anda melihat sedikit lebih dekat dengan kiraan, anda akan dapat mengetahui bagaimana ia berfungsi dan melihat bagaimana ia dibandingkan dengan sistem pengiraan berasaskan perpuluhan kami. Petunjuknya adalah ini; Sebaik sahaja anda kehabisan watak, anda hanya awalan watak pertama dengan watak pertama, menjadikan dua watak. Namun, bagaimana anda menulis 100? Adakah anda mesti bekerja sepanjang senarai? Mungkin kerana minda kita tidak digunakan untuk menghitung perkara menggunakan simbol -simbol ini.
Fikiran kita memahami perpuluhan, dan berjuang dengan yang lain X-base sistem berangka berasaskan di mana x tidak 10. Mungkin contohnya? Sila hitung )) (((A ==-() b ... (+ di mana kita telah menggunakan A untuk menunjukkan pendaraban, dan B adalah mudah ditambah. Tetapi tidak ada yang serupa mengenainya, betul? Namun, jika kita menukar ini kepada perpuluhan dan biasa kita + dan x simbol, kita mungkin tidak akan menemui persamaan ini dengan sukar.
Sekarang kita bersenjata dengan pemahaman tentang apa X-base betul -betul, selebihnya lebih mudah. Dan saya berjanji: tidak ada simbol yang lebih pelik untuk menyatakan nombor, sehingga kita sampai ke hexadecimal 😉
Binari
Sehingga komputer kuantum memukul kedai komputer tempatan kami, komputer kami agak terhad. Satu -satunya perkara, di sini sangat teras, yang mana komputer memahami adalah kuasa atau tiada kuasa. Tiada lagi! Komputer hanya memahami kuasa atau tidak ada kuasa, tetapi tidak "Fahami" Apa watak a adalah, atau apa digit 9 adalah. Semua perkara ini, dan banyak lagi (i.e. semua kod komputer) di terasnya dinyatakan sebagai kuasa atau kuasa tiada.
Satu unit penyimpanan dan ekspresi seperti itu dipanggil a bit. Sedikit adalah unit penyimpanan yang paling rendah, teras, penyimpanan komputer. A bit boleh menyimpan hanya satu 0 atau satu 1. Sebenarnya, ia tidak dapat menyimpan sifar atau satu, ia hanya dapat menyimpan kuasa (kami 1), atau tiada kuasa (kami 0). Anda boleh mula melihat bagaimana 2-asas, atau binari, berfungsi: ia hanya mempunyai dua ungkapan: 0 dan 1, tiada kuasa atau kuasa.
Sekiranya anda membayangkan ini dari segi perkakasan komputer fizikal, anda boleh membayangkan pemacu cakera keras jenis yang lebih tua sebagai plat yang penuh dengan banyak tempat kecil yang sama ada mempunyai kuasa (magnet) atau tidak mempunyai kuasa (tidak magnet). Sekiranya anda membayangkannya sebagai data yang mengalir di atas kabel, anda boleh membayangkannya sebagai kuasa atau tidak ada kuasa.
Oleh itu, mari kita mengira yang sama hingga 11 tetapi kali ini menggunakan hanya dua kaedah ekspresi yang mungkin, nombor dalam sistem berangka binari kami: 0 dan 1.
0: 0 1: 1 2: 10 3: 11 4: 100 5: 101 6: 110 7: 111 8: 1000 9: 1001 10: 1010 11: 1011
Di sebelah kiri kami mempunyai perpuluhan 10-asas, dan di sebelah kanan kami mempunyai 2-asas binari.
Sebaik sahaja anda Lihat, Ia mudah dikira: hanya bermula dengan 0 dan 1, dan perhatikan bagaimana 0 selalu mempunyai makna yang istimewa: semasa anda datang ke 2 Dalam perpuluhan, tidak 01 (i.e. watak pertama yang digunakan sebagai watak paling kiri), tetapi sebaliknya 10 sebagai 0 mempunyai nilai sebenar sifar. Dalam erti kata lain, anda tidak akan menulis: 0, 1, 2, 3, ..., 8, 9, 00 atau 01, kerana tidak masuk akal; seseorang akan menulis 10. Perkara yang sama berlaku di sini.
Perkara yang sama berlaku dalam sistem 5-asas kami di atas: kami menggunakan ) ( untuk menyatakan langkah seterusnya selepas semua digit kami digunakan, dan tidak (( yang tidak betul. Ia akan seperti menulis 00 dan bukannya 6.
Sebaik sahaja anda mengetahui langkah-langkah asas ini yang digunakan untuk semua sistem asas X, ia menjadi lebih mudah untuk dikira. Dan anda boleh menggunakan terus menambah watak paling kiri, dan menetapkan semula watak paling kanan yang sedang digunakan, apabila anda kehabisan langkah -langkah berangka seterusnya yang hanya menggunakan panjang yang anda miliki pada masa ini. Baca beberapa kali langkah binari dan lihatlah perkembangan, dan tidak lama lagi anda akan dapat bergantung pada binari, walaupun tanpa menggunakan jari. Sekiranya anda menggunakan jari, ingatlah untuk hanya menggunakan dua.
Hexadecimal
Jadi sekarang kita telah meneroka 10-base, 2-base (dan 5-base 😉 mari kita lihat sesuatu yang mungkin kelihatan ganjil lagi pada pandangan pertama: 16-asas. Bagaimana kita sesuai dengan 16 kemungkinan kombinasi berangka ke dalam satu watak? Selamat Datang ke HexadeCimal, yang menggunakan surat.
Mari kita buat kiraan mudah terlebih dahulu: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
16 aksara secara keseluruhan, sistem heksadesimal menggunakan A-F sebaik sahaja ia kehabisan cara untuk menyatakan nombor seterusnya Dalam siri ini. Mengira dari satu hingga 11 seperti yang kita lakukan sebelum ini akan dipertikaikan di sini, kerana ada 11 yang hanya dinyatakan oleh 'B'. Oleh itu, mari kita mulakan sedikit lagi dalam proses kali ini:
0: 0 1: 1 ... 9: 9 10: A ... 15: F 16: 10 17: 11
Di sebelah kiri kami mempunyai perpuluhan 10-asas, dan di sebelah kanan kami mempunyai hexadecimal 16-asas. Oleh itu, lebih mudah untuk diingat, ambil perhatian bahawa hexa-decimal membuat kita berfikir tentang 6-10.
Aduh! Sekarang kita berakhir dengan 10 dalam heksadesimal 16-asas yang sangat bernilai 16 Dalam perpuluhan 10-asas! Ini mungkin sedikit mengelirukan dan seseorang dapat melihat dengan segera keperluan untuk memahami dengan jelas sistem berangka yang kami bekerjasama untuk mengelakkan kesilapan yang mahal.
Banyak kalkulator dalam pelbagai sistem pengendalian mempunyai tetapan berasaskan pemaju atau komputer yang boleh diaktifkan untuk berfungsi dengan sistem berangka yang berbeza. Ada yang pergi satu langkah lebih jauh dan sangat jelas menunjukkan kepada anda berapa nombor yang akan diterjemahkan ke dalam pelbagai sistem berangka X-asas lain, seperti kalkulator hebat ini termasuk dalam Linux Mint 20:
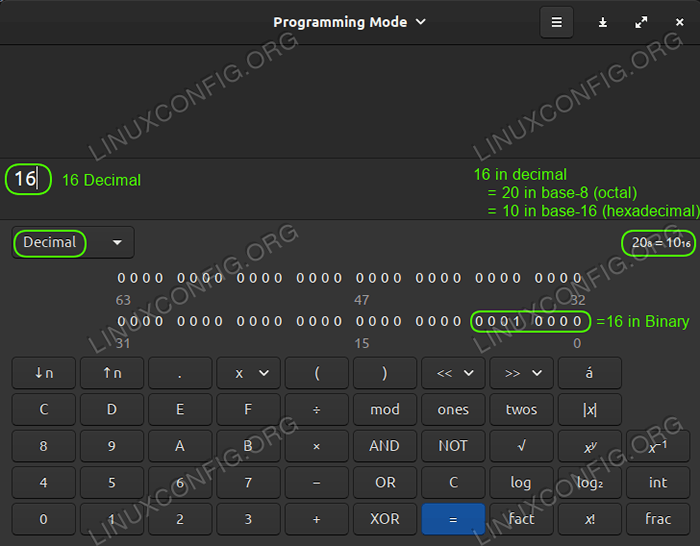Linux Mint 20 kalkulator menunjukkan perpuluhan, binari, heksadesimal, oktal sekaligus Oktal
Sekarang kita telah melihat sistem berangka sebelumnya, lebih mudah untuk melihat bagaimana kita boleh mengira dalam sistem 8-asas, dalam hal ini oktal, Sistem lain yang digunakan bersempena dengan dan oleh sistem pemprosesan komputer.
Di Octal, kami mempunyai 8 watak berangka yang menjadi 0, 1, 2, ..., 6, 7. Mari kita hitung hingga 11 dalam sistem berangka 8 asas, bermula pada 7:
7: 7 8: 10 9: 11 10: 12 11: 13
Di sebelah kiri kami mempunyai perpuluhan 10-asas, dan di sebelah kanan kami mempunyai octal 8-base.
Sekali lagi kita dapat melihat sedikit mengelirukan 10 dalam keadaan perpuluhan 10-asas 12 Dalam 8-base octal.
Mengapa begitu banyak sistem berangka?
Jadi mengapa terdapat banyak sistem berangka yang berbeza? Sebabnya mudah. Ingat bagaimana satu bit adalah kedai untuk meletakkan sifar binari atau satu? Nah, jika anda mengambil 8 bit, anda akan mempunyai satu bait, dan bait sering digunakan untuk menyatakan watak-watak alfa-numerik tunggal yang mudah. Sekiranya anda berfikir tentang bagaimana 8 benar -benar berada di dasar ini, ia tidak sepatutnya menjadi regangan untuk melihat oktal (8) sesuai dengan sistem berangka yang digunakan pada komputer.
Seterusnya kita mempunyai heksadesimal, yang sebenarnya 2 x 8 = 16 aksara. Dan di sini, kami mempunyai 16 bit (atau 2 bait) yang diwakili sebagai satu watak. Semuanya tergantung bersama, dan benar-benar dimainkan apabila anda mempertimbangkan bagaimana watak-watak alfa-angka digunakan dan diproses di dalam sistem komputer. Contohnya, beberapa watak khas (seperti contoh watak Jepun atau Cina) mungkin memerlukan dua atau tiga bait untuk menyimpannya (berbilang bait).
Pelbagai sistem berangka memudahkan pelbagai jenis aliran data yang berlaku dalam komputer, dan bergantung pada aliran di tangan, dan mana -mana algoritma komputer yang sepadan yang dipilih atau digunakan, pelbagai pengoptimuman mungkin bergantung pada sistem berangka yang anda gunakan. Kebanyakan bahasa membangun mempunyai, sebagai contoh, pemprosesan binari dan berpotensi heksadesimal yang sangat dioptimumkan selain pemprosesan perpuluhan.
Kesimpulan
Dalam artikel ini, kami menyelam ke dalam sistem berangka 2-base, 10-base, 16-base, dan 8-base, sebagai binari (2), perpuluhan (10), heksadesimal (16) dan oktal (8). Kami melihat jenis sambungan di antara ini, dan bagaimana melakukan pengiraan mudah dalam semua sistem ini.
Belajar sedikit lebih lanjut mengenai bagaimana komputer berfungsi sering membantu, terutamanya ketika membuat program komputer pertama atau teori pemahaman. Apabila seseorang menjadi pemaju sepenuh masa, pada tahap itu semua sistem ini adalah sifat kedua, dan mereka sering digunakan dalam kod sebenar.
Tolong tinggalkan komen kami dengan pandangan anda mengenai sistem berangka ini! Dan jika anda sudah bersedia untuk mempelajari lebih banyak perkara yang menarik, lihatlah manipulasi data besar kami untuk keseronokan dan keuntungan bahagian 1 artikel! Nikmati!
Tutorial Linux Berkaitan:
- Tutorial Debugging GDB untuk Pemula
- Pengenalan kepada Automasi, Alat dan Teknik Linux
- Perkara yang hendak dipasang di Ubuntu 20.04
- Mint 20: Lebih baik daripada Ubuntu dan Microsoft Windows?
- Sistem Hung Linux? Cara melarikan diri ke baris arahan dan ..
- Perkara yang perlu dilakukan setelah memasang ubuntu 20.04 Focal Fossa Linux
- Cara membuat pengiraan perpuluhan di bash menggunakan bc
- Menguasai Gelung Skrip Bash
- Ubuntu 20.04 Panduan
- Perkara yang perlu dilakukan setelah memasang Ubuntu 22.04 Jur -ubur Jammy ..